Amid the post–New Year spate of project roundups, I discovered Luke Pattons’ Canvas Cards project, and through it some mesmerizing procedural animations by Raven Kwok.
— Raven Kwok (@RavenKwok) April 14, 2019
Pushed it to three-dimension. Tolerable, yet still much room for improvement regarding vertical displacement. pic.twitter.com/Zdt0Aa8ZQL
— Raven Kwok (@RavenKwok) April 16, 2019
I didn’t find much on how Kwok implemented the animations beyond his comment that “the visual’s core structure is a K-D tree”. So I decided to experiment with k-d tree animation myself.
A k-d tree is a binary tree structure that encodes k-dimensional points to define a partitioning of a k-dimensional space. Sequential levels of the tree contain the median points of subsets of the points in alternating dimensions, carving up progressively smaller areas. The trees are commonly used for nearest-neighbor search, but here our goal is to use them to drive visually interesting transformations of geometrical shapes.
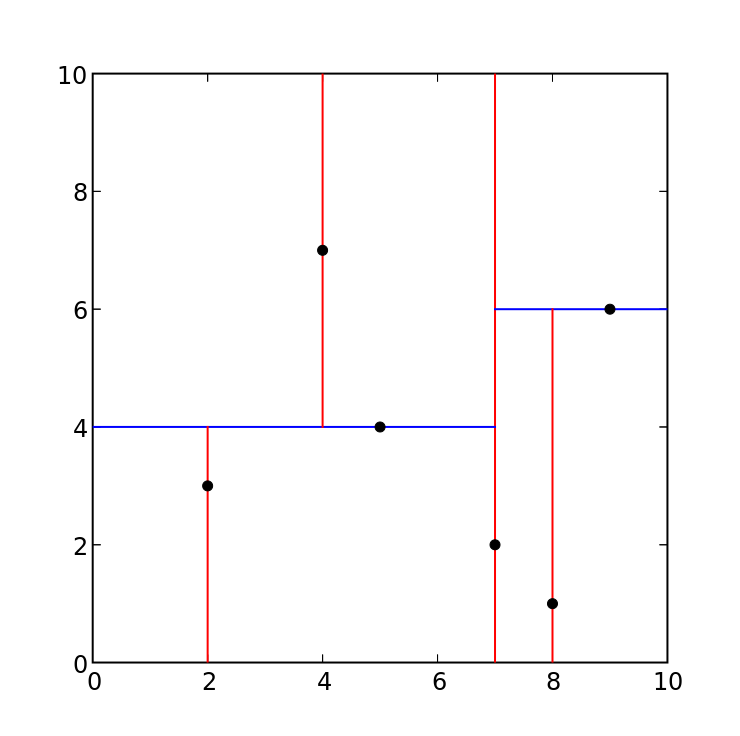
It was pretty easy to implement some basic logic to render a 2-d tree to an HTML5 canvas; Wikipedia has some working code snippets which build the tree by recursing over the nodes. In my first attempt to animate it I picked two arrays of points, interpolating between them and rendering the k-d tree that results from each interpolation:
The results are not great, since the lines of the tree are not continuous throughout the animation—as points shift, their positions in the tree will eventually change, causing the lines to jump.
My next idea was to interpolate the values in the tree directly. I build k-d trees for an initial and final set of points and then render trees which tween the values of the isomorphic nodes. The interpolated trees aren’t proper k-d trees, but they’re visually similar and give a nice, continuous animation.
By the end of what had turned out to be a rather long Friday night of experimentation, I had built a moderately engaging little animation. First I switched to coloring the rectangles formed by the tree rather than the lines. Then I dialed up the number of points used to generate the tree and punched up the timings. Finally I switched from the RGB palette I’d used for testing to something a bit easier on the eyes.
Having made it this far brought home to me the range of choices that influence these animations’ feel. The selection of color, gradient and texture (there’s a graininess superimposed on Kwok’s images), along with the use of negative space and staggered transitions, do a lot to make Kwok’s animations engaging. The ability to incorporate improper trees in the animation also intrigues me—it’s a natural step from interpolating points between k-d trees to decomposing arbitrary shapes into k-d–defined blocks and back again. My next explorations, if I come back to this concept, will probably take that idea further.